ここでは、重積分を使って物体の重心位置を求める方法を解説します。また、例として扇形や半円板の面積の求め方も記載しています。
質量 \(m_i\)、重心位置 \((x_i, y_i)\) の物体が、いくつか結合してひとつの塊になっているとします。結合した物体の全質量が \(M\) とすると、その重心位置 \((x_G, y_G)\) は次の式で求められます。
\[ x_G = \frac 1M \sum x_i m_i \]
\(y_G\) も同様の式になります。ただし、物体の重心が \(x\) 軸上にある場合は \(y_G = 0\) です。
\[ x_G = \frac 1M \int x \ \mathrm dm \]
しかし、このままでは計算できないので式を変形していきます。
まず、物体は一様である(密度 \(\rho\) が一定)とします。物体の体積を \(V\) とすると、質量と体積の関係から \(\mathrm dm = \rho \ \mathrm dV\) となるので、次式のように変形できます。
\[ \begin{align} x_G &= \frac 1M \int x \ \mathrm dm \\ &= \frac{\rho}{M} \int x \ \mathrm dV \\ &= \frac 1V \int x \ \mathrm dV \\ &= \frac 1V \iiint x \ \mathrm dx \ \mathrm dy \ \mathrm dz \end{align} \]
さらに、物体が薄板である(厚さ \(z\) を無視できる)場合は、物体の面積を \(S\) として、次のように書けます。
\[ x_G = \frac 1S \iint x \ \mathrm dx \ \mathrm dy \]
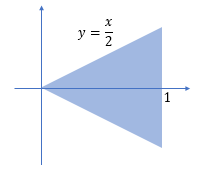
計算を始める前に、積分の順序を考えます。今回は、微小面積 \(\mathrm dx \ \mathrm dy\) を \(y\) で積分してから \(x\) で積分することにします。
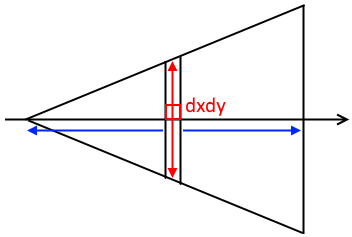
このとき、\(y\) の積分区間は \(-x/2 < y < x/2\) で、\(x\) の積分区間は \(0 < x < 1\) です。\(y\) から積分するので、式の最後の部分は \(\mathrm dy \ \mathrm dx\) と書きます。
\[ \begin{align} x_G &= \frac 1S \int_0^1 \int_{-x/2}^{x/2} x \ \mathrm dy \ \mathrm dx \\ &= \frac 1S \int_0^1 x^2 \ \mathrm dx \\ &= \frac 1S \frac 13 \\ \end{align} \]
ここで、三角形の面積は \(S = 1/2\) なので、\(x_G\) は次の値になります。
\[ x_G = \frac 2 3 \]
また、\(x = r \cos \theta\) より、重心位置は次のように書けます。
\[ \begin{align} x_G &= \frac 1S \iint x \ \mathrm dx \ \mathrm dy \\ &= \frac 1S \iint ( r \cos \theta ) \ r \ \mathrm d\theta \ \mathrm dr \\ &= \frac 1S \iint r^2 \cos \theta \ \mathrm d\theta \ \mathrm dr \end{align} \]
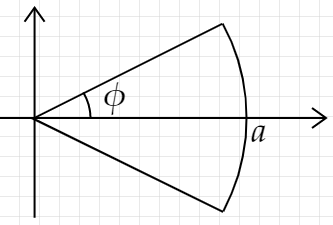
積分区間は \(-\phi < \theta < \phi\) および \(0 < r < a\) です。区間に変数が含まれていないので、積分順序は不問です。
\[ \begin{align} x_G &= \frac 1S \int_0^a \int_{-\phi}^{\phi} r^2 \cos \theta \ \mathrm d\theta \ \mathrm dr \\ &= \frac 1S \int_0^a r^2 \ \mathrm dr \int_{-\phi}^{\phi} \cos \theta \ \mathrm d\theta \\ &= \frac 1S \frac{a^3}{3} 2 \sin \phi \end{align} \]
ここで、扇形の面積 \(S\) は次のように表せます。
\[ S = \pi a^2 \frac{2 \phi}{2 \pi} = a^2 \phi \]
以上より、扇形の重心位置 \(x_G\) は次の通りです。
\[ x_G = \frac{2a \sin \phi}{3 \phi} \]
ここで、特に半円板の重心位置は、\(\phi = \pi / 2\) を代入して次のようになります。
\[ x_G = \frac{4a}{3 \pi} \]
総和による重心位置の計算
積分を使う前に、まずは総和によって重心位置を求める方法を考えてみます。質量 \(m_i\)、重心位置 \((x_i, y_i)\) の物体が、いくつか結合してひとつの塊になっているとします。結合した物体の全質量が \(M\) とすると、その重心位置 \((x_G, y_G)\) は次の式で求められます。
\[ x_G = \frac 1M \sum x_i m_i \]
\(y_G\) も同様の式になります。ただし、物体の重心が \(x\) 軸上にある場合は \(y_G = 0\) です。
積分による重心位置の計算
ここで、各物体が微小な質量 \(\mathrm dm\) を持って連続的に結合していると考えると、上記の総和の式が、次の積分の式に変わってきます。\[ x_G = \frac 1M \int x \ \mathrm dm \]
しかし、このままでは計算できないので式を変形していきます。
まず、物体は一様である(密度 \(\rho\) が一定)とします。物体の体積を \(V\) とすると、質量と体積の関係から \(\mathrm dm = \rho \ \mathrm dV\) となるので、次式のように変形できます。
\[ \begin{align} x_G &= \frac 1M \int x \ \mathrm dm \\ &= \frac{\rho}{M} \int x \ \mathrm dV \\ &= \frac 1V \int x \ \mathrm dV \\ &= \frac 1V \iiint x \ \mathrm dx \ \mathrm dy \ \mathrm dz \end{align} \]
さらに、物体が薄板である(厚さ \(z\) を無視できる)場合は、物体の面積を \(S\) として、次のように書けます。
\[ x_G = \frac 1S \iint x \ \mathrm dx \ \mathrm dy \]
[例] 三角形の重心位置を求める
例として、\(y = x/2,\ y = -x/2,\ x = 1\) の直線に囲まれた二等辺三角形の薄板の重心位置を考えてみます。
計算を始める前に、積分の順序を考えます。今回は、微小面積 \(\mathrm dx \ \mathrm dy\) を \(y\) で積分してから \(x\) で積分することにします。

このとき、\(y\) の積分区間は \(-x/2 < y < x/2\) で、\(x\) の積分区間は \(0 < x < 1\) です。\(y\) から積分するので、式の最後の部分は \(\mathrm dy \ \mathrm dx\) と書きます。
\[ \begin{align} x_G &= \frac 1S \int_0^1 \int_{-x/2}^{x/2} x \ \mathrm dy \ \mathrm dx \\ &= \frac 1S \int_0^1 x^2 \ \mathrm dx \\ &= \frac 1S \frac 13 \\ \end{align} \]
ここで、三角形の面積は \(S = 1/2\) なので、\(x_G\) は次の値になります。
\[ x_G = \frac 2 3 \]
極座標の積分
半円板や扇形の重心を計算するときは、極座標を利用して積分すると簡単に計算できます。極座標では、微小面積を \(\mathrm dx \ \mathrm dy\) ではなく \(r \ \mathrm d\theta \ \mathrm dr\) と表します。また、\(x = r \cos \theta\) より、重心位置は次のように書けます。
\[ \begin{align} x_G &= \frac 1S \iint x \ \mathrm dx \ \mathrm dy \\ &= \frac 1S \iint ( r \cos \theta ) \ r \ \mathrm d\theta \ \mathrm dr \\ &= \frac 1S \iint r^2 \cos \theta \ \mathrm d\theta \ \mathrm dr \end{align} \]
[例] 扇形の重心位置を求める
例として、半径 \(a\)、中心角 \(2 \phi\) の扇形の重心位置を求めます。
積分区間は \(-\phi < \theta < \phi\) および \(0 < r < a\) です。区間に変数が含まれていないので、積分順序は不問です。
\[ \begin{align} x_G &= \frac 1S \int_0^a \int_{-\phi}^{\phi} r^2 \cos \theta \ \mathrm d\theta \ \mathrm dr \\ &= \frac 1S \int_0^a r^2 \ \mathrm dr \int_{-\phi}^{\phi} \cos \theta \ \mathrm d\theta \\ &= \frac 1S \frac{a^3}{3} 2 \sin \phi \end{align} \]
ここで、扇形の面積 \(S\) は次のように表せます。
\[ S = \pi a^2 \frac{2 \phi}{2 \pi} = a^2 \phi \]
以上より、扇形の重心位置 \(x_G\) は次の通りです。
\[ x_G = \frac{2a \sin \phi}{3 \phi} \]
ここで、特に半円板の重心位置は、\(\phi = \pi / 2\) を代入して次のようになります。
\[ x_G = \frac{4a}{3 \pi} \]


コメント
コメント一覧 (2)
ありがとうございます。
重心の位置が、2a / 3 となるのは少し不思議ですね。。
なんとなく、棒形状に成るので、重心の位置が、a/2 となるような気がするのですが。。
あくまで、扇に対する重心なので、a/2とならないのでしょうね。